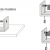
1Q20.17 Torque e aceleração angular
Uma massa está pendurada na extremidade de um fio que passa por um eixo. Um paralelepípedo de madeira está fixo nesse eixo.
Quando a massa é solta a partir de determinada altura, o peso dela produz um torque sobre o eixo que passa a girar junto com o bloco. A aceleração angular que o bloco adquire depende do seu momento angular.
Em cada montagem, o eixo atravessa diferentes faces de blocos idênticos que terão, portanto, diferentes momentos de inércia. Quanto maior for o momento de inércia do bloco em torno do eixo, menor será a aceleração angular que ele adquire.
Mais informações
A aceleração angular [m]\alpha[/m] de um bloco com momento de inércia [m]I[/m] é dada pela segunda lei de Newton para o movimento de rotação, [m]\alpha = \frac{T}{I} [/m], em que [m]T[/m] é o torque sobre o eixo do bloco.
Esse movimento pode ser analisado também considerando-se que a energia potencial gravitacional da massa é convertida em energia rotacional do bloco, ou seja,
[m] mgh = 1/2 Iω²[/m], em que [m]\omega[/m] é a velocidade angular que o bloco adquire quando a massa é solta de uma altura [m]h[/m].
Tempo de preparo: Pronta entrega
